Materi Matriks Lengkap Dan Contohnya

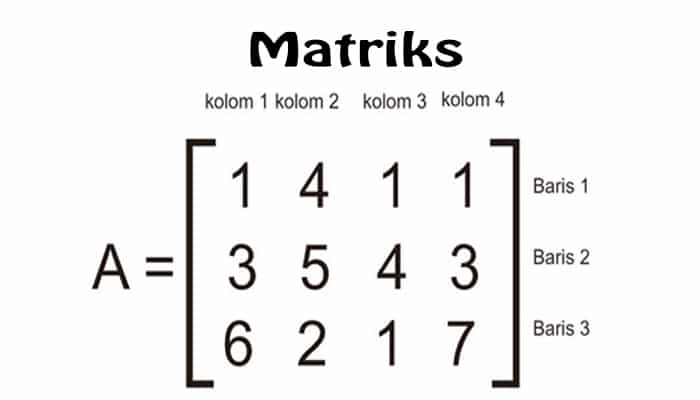
 Matriks dalam matematika merupakan kumpulan bilangan, simbol atau ekspresi berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat pada suatu matriks disebut dengan elemen atau disebut juga anggota dari suatu matriks. Contoh matriks dengan 2 baris dan 3 kolom yaitu sebagai berikut

Matriks banyak dimanfaatkan untuk menyelesaikan berbagai permasalahan matematika misalnya dalam menemukan solusi masalah persamaan linear, transformasi linear yakni bentuk umum dari fungsi linear contohnya rotasi dalam 3 dimensi. Matriks juga seperti variabel biasa, sehingga matrikspun dapat dimanipulasi misalnya dikalikan, dijumlah, dikurangkan, serta didekomposisikan. Menggunakan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur.

adversitemens

Operasi Dasar Matriks :

1. Penjumlahan dan Pengurangan Matriks

Penjumlahan serta pengurangan dalam matriks hanya dapat dilakukan apabila kedua matriks mempunyai ukuran atau tipe yang sama. Elemen-elemen dalam suatu matriks yang dijumlahkan atau dikurangan yaitu elemen yang memilki posisi/letak  yang sama.

representasi dekoratifnya sebagai berikut

2. Perkalian Skalar

Perkalian matriks dilakukan dengan cara tiap baris dikalikan dengan tiap kolom, selanjutnya dijumlahkan pada kolom yang sama

 dan 

maka 

contoh perhitungan :

 

Ordo suatu matriks merupakan bilangan yang menunjukan banyaknya baris (m) dan banyaknya kolom (n). Sebagai contoh :  merupakan matriks berordo 3×2

 

Matriks Identitas

Matriks Identitas adalah matriks yang anggota pada diagonal utamanya selalu 1

Matriks Transpose (A^t)

Matriks transpose merupakan matriks yang mengalami pertukaran elemen dari kolom menjadi baris atau sebaliknya. Contoh :

maka matriks transposenya (A^t) adalah 

Contoh – contoh :

1. Kesamaan Dua Matriks

Tentukan nilai 2x-y+5z!

Jawab:

 maka 

 maka 

 maka 

3. Contoh Perkalian matriks dengan variabel

4. 

 

Determinan Suatu Matriks

Untuk menentukan determinan dari suatu matriks dapat digunakan beberapa cara :

1. Misalnya terdapat matriks  yang berordo 2×2 dalam menentukan determinan dari matrikas A yang biasa ditulis |A| adalah

 

2. Metode Sarrus

Misalnya terdapat  maka untuk menentukan nilai determinan dari matriks A tersebut

Ubah matriks dalam bentuk seperti diatas selanjutnya perhitungannya dengan cara menambahkan elemen dari kiri atas kekanan bawah (mulai dari a → e → i, b → f → g, dan c → d → h) kemudian dikurangi dengan elemen dari kanan atas kekiri bawah (mulai dari c → e → g, a → f → h, dan b → d → i) maka akan menjadi

Sebagai contohnya

maka tentukan 

 

3. Metode Ekspansi Baris dan Kolom

Jika diketahui  maka untuk menentukan determian dari matriks P

 

Matriks Singular

Matriks Singular yaitu matriks yang nilai determinannya 0.

Sebagai contoh

Jika A matriks singular, tentukan nilai x!

Jawab:

 vs 

Invers Matriks

Misalnya diketahui   maka invers dari matriks A

Sifat-sifat dari invers suatu matriks :

Persamaan Matriks

Tentukan X matriks dari persamaan:

• Jika diketahui matriks A.X=B

• Jika diketahui matriks X.A=B